My research focuses on designing and implementing automated reasoning tools for software engineers. The fundamental principle behind my work is that the full automated reasoning stack should be tailored to users’ needs rather than the other way around. During my Ph.D., I built a full automated reasoning stack for the formal verification of distributed systems.

Designing and implementing distributed systems is still an enormous task for software engineers. Much of this challenge stems from bugs arising from complex combinations of machine failures and message orderings that are difficult for humans to reason about manually [Gabrielson 2019]. As distributed systems become increasingly critical infrastructure, engineers will need more computational support to build and deploy them correctly.

Automated reasoning engines promise to be the computational support that engineers need. These engines can solve tedious, mission-critical logic problems billions of times a day (e.g., Rungta [2022]). In the domain of distributed systems specifically, these tools have helped find bugs and prove the correctness of industrial systems (e.g., Newcombe et al. [2015]). Unfortunately, despite their power and flexibility, adoption of automated reasoning engines remains low for one fundamental reason. Today, successful users must be experts in their application domain and automated reasoning—a rare combination. Specifically, users must be able to precisely describe their problem in a formal language, like first-order logic, and know enough about automated reasoning to make sure their encoded problem is practically solvable.¹

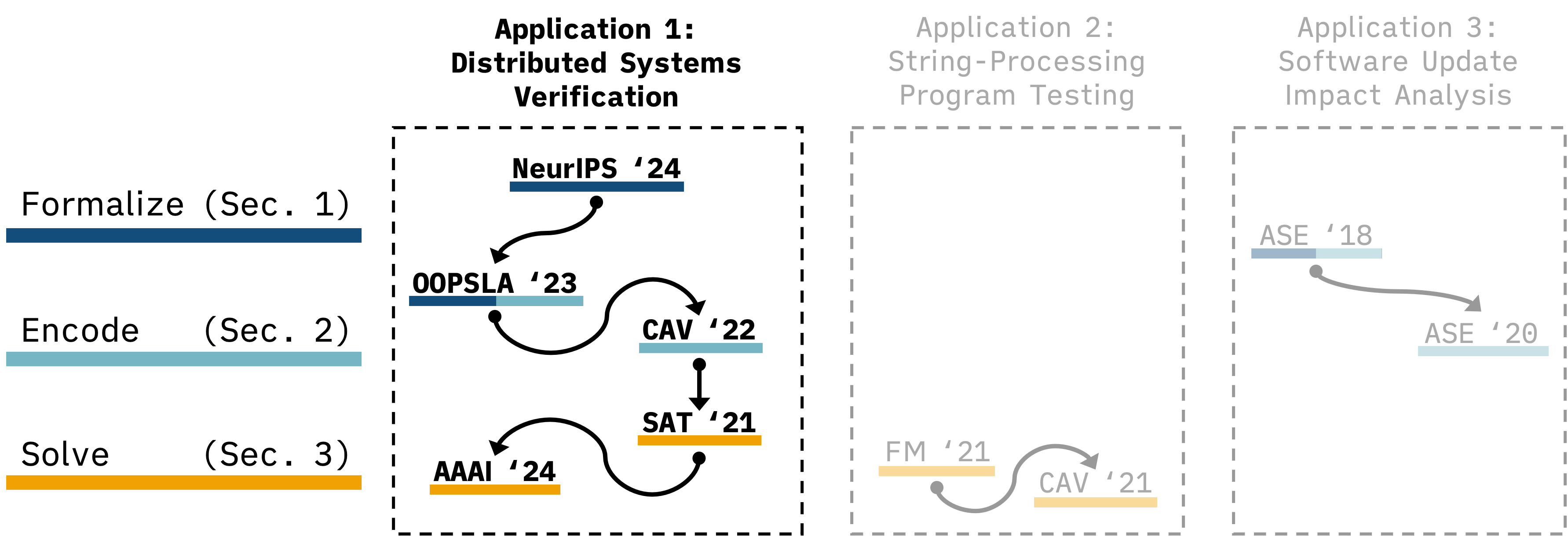
The stack I built during my Ph.D. reduces the need for automated reasoning expertise by partially automating the interaction with automated reasoning tools, allowing engineers to verify their systems in a modeling language they are already using, and providing the fastest solver in the world for a relevant fragment of logic. Fig. 1 illustrates three key layers of the stack and lists the venues where I published my contributions. Over the subsequent three sections, I describe each layer and the corresponding work in order, from top to bottom of the figure. I conclude in Sec. 4 with future work.

1 Formalize: Semi-Automated Modeling

The first layer in Fig. 1 corresponds to the process of formally modeling and specifying a domain-specific task. For example, in distributed systems, this could be modeling a leader election protocol and specifying that at most one leader is elected. This process usually requires the use of a verification language and can be intricate. In our NeurIPS ’24 paper [Mora et al. 2024], we presented an approach to build text-to-formal-model tools that help automate this process. These tools must understand natural language, and so we depend on large language models (LLMs). The main challenge is that LLMs struggle to generate code in low-resource programming languages, like most verification languages. Existing solutions either provide no guarantees and perform poorly (e.g., fine-tuning and prompting) or are not expressive enough to capture real modeling languages (e.g., constrained decoding with context-free languages).

The first key idea behind our approach comes from natural programming elicitation, a class of studies that help programming language designers understand how programmers naturally approach problems from a given programming domain [Myers et al. 2004]. Programming language designers use the results of these studies to create languages aligned with users’ expectations, leading to less programming friction and more effective developers. We borrowed this idea for the setting where LLMs are the “users.” Akin to uncovering what human users find natural for a given domain, we uncover what LLMs find “natural.” Specifically, our first insight is to embrace LLM’s tendencies and design an intermediate language that aligns with the LLM’s output distribution for tasks in our domain.

Our first key idea makes it possible for LLMs to generate reasonable programs, but it presents a new challenge: different languages have different features, like type systems, that make translation difficult. The second key idea behind our approach is to use an automated reasoning engine—a MAX-SMT solver in this case—to identify the minimal set of locations in the intermediate program that prevent a correct translation to the target language. We then repair these locations using deductive techniques and LLM calls, repeating the process as necessary. This symbolic component guarantees that generated programs pass all compiler checks, including type checking, for the target modeling language.

We implemented a prototype of our approach in a tool called Eudoxus, which translates natural language text into UCLID5 programs. UCLID5 is an open-source formal modeling language and verification framework that supports several projects and whose development I help lead. We described UCLID5 in our CAV ’22 paper [Polgreen et al. 2022]. Eudoxus outperforms fine-tuning, self-repair, few-shot prompting, and chain-of-thought prompting over test problems collected from three well-known textbooks. Specifically, our tool correctly solved 33% of textbook problems, while the next best approach solved only 3%. Eudoxus is open-source.

2 Encode: Domain-Specific Verification Engine

The second layer in Fig. 1 corresponds to encoding the formalized task into logical queries. This is exactly what UCLID5 does: it implements verification and synthesis algorithms that iteratively call a satisfiability modulo theories (SMT) solver. However, UCLID5 is a general-purpose verification framework whose programming paradigm does not match what distributed systems engineers are used to using. Specifically, modern programming languages provide software engineers with a choice of different distributed systems programming paradigms. Two popular paradigms include the actor model, supported natively by e.g., Erlang; and the model of communicating sequential processes, supported natively by e.g., Go. UCLID5, like all other popular verification languages, supports neither of these popular paradigms.²

In our OOPSLA ’23 paper [Mora et al. 2023], we took a language for modeling communicating state machines, called P, and added support for formal verification through proofs-by-induction. We call the resulting open-source tool the PVerifier. P is more similar to the actor model than any existing verification language, making the modeling process more direct for distributed systems engineers. Before our work, P had support for explicit-state model checking (similar to testing), and engineers inside Amazon were already successfully using it to find bugs in real systems [Desai 2023; Terry 2024]. Our work allows these same engineers to write proofs of correctness in the modeling language they are already using.

The main challenge in verifying P programs is that they explicitly model message passing. Proofs, therefore, have to consider lemmas over the low-level details of single messages. To remedy this, we provide users with language support for reasoning about sequences of logically related messages, called message chains. Message chains are related to message sequence charts [ITU-T 2011] from the software engineering community and choreographic programming languages [Montesi 2014] from the programming languages community. Both message sequence charts and choreographic programming offer developers a way to reason about explicit message passing but with the context of how messages flow through the system in question. We use message chains to bring these same ideas to formal verification.

We implemented the PVerifier as part of the P language toolchain using UCLID5 as a backend. We evaluated the PVerifier by verifying systems from related work and two systems inside Amazon. We found that, with message chains, proofs require a similar number of lemmas than more abstract frameworks, verification time is comparable, and some lemmas can be automatically learned using classic learning algorithms, like Angluin [1980]. Since publication, we have invested significant engineering time to improve modular reasoning, support parallel solving, and design a novel proof caching mechanism. These extensions increase scalability and are powering an exciting ongoing verification effort inside Amazon today.

3 Solve: Eager Decision Procedure and Algorithm Selection

The third layer in Fig. 1 corresponds to solving the generated logical queries. The PVerifier, through UCLID5, generates SMT queries that ask, “is there a counterexample to induction?” In our AAAI ’24 paper [Shah et al. 2024], solver, called Algaroba, that can answer these questions. Specifically, Algaroba handles SMT queries with algebraic data types (ADTs), which naturally capture programming data structures, like message chains, and appear extensively in the questions generated by the PVerifier, Eudoxus, and other distributed systems verification projects (e.g., Zhang et al. [2024]). Algaroba is the fastest solver available: it won the quantifier-free ADT track at the 2024 SMT Competition [Bromberger et al. 2024].

Algaroba takes an eager approach to solving queries. Specifically, it takes a quantifier-free query containing ADTs and translates it to a quantifier-free query without ADTs that existing non-ADT solvers can handle. Algaroba eliminates ADTs by replacing them with uninterpreted sorts and functions along with a finite number of quantifier-free axioms. The key technical challenge with eagerly solving ADT queries is that this kind of translation seems like it should require an unbounded number of axioms (e.g., lists can be arbitrarily long, but no list is equal to any of its sub-lists). Despite this, we proved that our finite translation is sound and complete.

Most other automated reasoning engines in this space take a lazy approach. In the lazy approach, theory axioms are introduced as needed instead of upfront. Since Algaroba takes a fundamentally different approach to existing tools, its performance profile is unique: Algaroba solves many queries that no other solver succeeds on, and other solvers succeed on queries for which Algaroba fails. This phenomenon is common for satisfiability solvers. The problem is that, for any given query, it is hard to know what solver will succeed ahead of time.

In our FM ’21 paper [Mora et al. 2021], we defined three solving algorithms for satisfiability queries over the theory of strings and provided a fixed classifier for deciding when to use what algorithm. In our SAT ’21 paper [Pimpalkhare et al. 2021], we generalized that work to an online learning scheme that supports any logical theories. Our open-source tool, called MedleySolver, takes a stream of queries from a given domain. For each query, MedleySolver picks a solver to execute and learns from the result. Over time, without any human expertise, MedleySolver automatically discovers the best solver for queries in the target domain. Specifically, MedleySolver solves more queries than any individual solver using significantly less time.

4 Future Work

Moving forward, I will build on the fundamental principle in my dissertation research: the full automated reasoning stack should be tailored to users’ needs rather than the other way around. I am excited to continue improving automated reasoning for distributed systems experts, expanding my work to new domains, and developing new neuro-symbolic reasoning approaches.

New Stacks For New Domains. Automated reasoning engines do not currently support many programming paradigms and features. For example, OCaml’s new concurrency model [Sivaramakrishnan et al. 2021], based on algebraic effects, is popular in programming language circles but has gained much less attention in the automated reasoning community. Therefore, today, engineers have few choices when it comes to proving the correctness of these programs. I am interested in exploring new programming language paradigms and features, like algebraic effects, and building full automated reasoning stacks for their users.

Declarative Eager Solvers. Improving the automated reasoning stack for distributed systems and creating stacks for new domains will depend on the availability of fast solvers. The problem is that we do not know what logical theories and fragments we will need to support or what industrial queries will look like tomorrow. This is true for the whole field of automated reasoning: the demand for solvers is growing in often unpredictable directions. I aim to meet this demand through eager solvers. Eager solvers are promising for distributed solving, but handling theory combinations is currently challenging. I am particularly excited about facing these challenges by generating eager solvers from declarative specifications.

Neuro-Symbolic Reasoning. My text-to-formal-model work has exciting implications for neuro-symbolic reasoning. For example, Olausson et al. [2023] follow the tool-use paradigm to solve natural language word problems by equipping an LLM with an automated theorem prover tool. These same authors find that one of the biggest limitations of this approach is that LLMs frequently generate syntactically incorrect calls to the theorem prover—precisely the problem we solved with Eudoxus for UCLID5. I aim to explore these exciting implications, particularly for reasoning about distributed systems described in documentation using natural language and diagrams. The dream is that developers will be able to ask questions about their documented designs and get meaningful feedback powered by domain-specific automated reasoning engines.

References